Seit Beginn der Astronomie waren Winkelmessungen die Vorausetzung für die Bestimmung der Position der Gestirne. Um Winkel zu diesem Zweck möglichst genau bestimmen und dokumentieren zu können, waren geometrische Hilfsmittel erforderlich. Die indischen Mathematiker und Astronomen übernahmen schon sehr früh die mathematischen Erkenntnisse der Griechen.

Das arabische Wort "dschaib" bedeutet Meerbusen und als im 12. Jahrhundert versucht wurde, mathematische Begriffe in das Lateinische zu übersetzen, wurde "dschaib" mit der lateinischen Bezeichnung für Meerbusen (Sinus) übersetzt. Es ist Georg von Peuerbach zu verdanken, dass die Sinusrechnung zu neuer Entfaltung gebracht wurde.  Er führte eine völlige Neuberechnung der trigonometrischen Zahlenwerte durch, welche zu einer entscheidenden Verbesserung der Genauigkeit führte.
Das wirkllich entscheidend Neue dabei ist die neu berechnete Sinus-Tafel. In seinem "EPITOMA" beschrieb er die vorteilhafte Anwendung der Sinusrechnung in der Trigonometrie.

Aufbauend auf den trigonometrischen Berechnungen Peuerbachs schuf Regiomontanus das erste umfassende Werk über Dreiecksberechnungen "DE TRIANGULIS OMNIMODIS LIBRI QUINQUE", welches die Grundlage für die abendländische Trigonometrie und auch noch für spätere Mathematikergenerationen bildete. In diesem Werk findet sich zum ersten Mal der für die Perfektionierung der  Sinusrechnung entscheidende "Cosinus Satz".

In zwei bemerkenswerten Arbeiten entwickelte Peuerbach eine besonders raffinierte mathematische Beziehung zur Berechnung der Sonnenhöhe:
sin h (cos b - 1) = sin H (cos b - cos t)
Der Cosinus, vorher sinus versus genannt, wurde bald zum gleichwertigen Partner des Sinus. Das Wort Cosinus ist aus dem Begriff "Complimenti Sinus" abgeleitet.

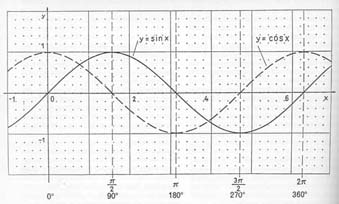
Trägt man die zu jedem y-Wert zugehörigen Sinuswerte auf der x-Achse ein, so entsteht eine auffallende Reihen von Punkten. Verbindet man sie, so bildet sich eine wellenförmige Kurve: die Sinuskurve. Nimmt man analog die Cosinuswerte so erhält man die Cosinuskurve.
Damit erschließt sich die Möglichkeit der Berechnung der Wellen und Schwingungen. Die Nutzung dieser Wellen (Rundfunk, Fernsehen, Radarwele, etc...) ist aus unserem Leben nicht mehr wegzudenken. Georg von Peuerbach hat mehr für die Anwendung und Verbreitung der Sinus-Cosinus-Rechnung geleistet als jeder andere Mathematiker vor ihm.